Un prototype programmable pour concrétiser la machine de Turing

Accueil

Alan TURING

Histoire

Machine de Turing

Le prototype expérimental réalisé

Quelques diagrammes de machines de Turing pour ce prototype

Interventions

Presse

Simulateur

Nouvelle machine

Machines

Idées

Descriptif

Fonctionnement

Technologie

1ère machine de Turing

Facile

Calculateurs

Suites

Intéressant

Lycées

Universités

Conférences

Vidéos

Contact

Description de la machine de Turing C'est un prototype de la machine imaginée par Alan Turing pour modéliser le concept d'algorithme et donner une réponse négative au problème de la décision en logique du premier ordre posé quelques années auparavant par Hilbert et Ackermann. Pour simplifier, est-il possible de trouver une méthode "effectivement calculable" pour décider si une proposition est démontrable ou non ? Ce prototype est directement issu de la description qu'il a donnée dans son article publié en 1937 intitulé : On computable Numbers, with an Application to the Entscheidungsproblem. Cette machine est en fait le modèle le plus simple que l'on puisse concevoir et qui satisfait aux critères informels mais universels qui caractérisent un algorithme. C'est un modèle universel de calcul et elle peut calculer tout ce que n'importe quel ordinateur physique peut calculer. Inversement ce qu'elle ne peut pas calculer ne peut l'être non plus par un ordinateur. Elle constitue un modèle idéal pour raisonner autour de la notion d'algorithme de calcul ou de démonstration. a-machine "Nous pouvons comparer un homme en train de calculer un nombre réel à une machine qui ne peut prendre qu'un nombre fini d'états q1: q2. Qn ....; qui seront appelé "m-configurations". La machine comporte un "ruban" (l'analogue de papier) qui la traverse, divisé en sections (appelé "carrés") dans lesquels on peut inscrire un "symbole". A tout moment, un seul carré peut se trouver "dans la machine" on nomme T(r) le symbole qu'il porte. Ce carré est le "carré traité" et le symbole qu'il porte, le "symbole traité". Le symbole traité est le seul dont la machine est pour ainsi dire "directement consciente". Cependant, en changeant d'état-m, la machine peut se souvenir de certains des symboles qu'elle a vus (balayés) avant. A tout instant, le comportement de la machine est déterminé par la m-configuration qn et le symbole lu T(r). Cette paire de qr, T(r) sera appelé la "configuration", cette configuration détermine le comportement de la machine. Selon les cas, la machine pourra écrire un symbole dans un carré vierge (blank), effacer un symbole déjà écrit dans un carré, ou bien la machine pourra changer de carré par un déplacement d'une case à gauche ou à droite. De plus, la m-configuration peut être changée. Si à chaque étape, le comportement de la machine est complétement déterminé par sa configuration, nous appellerons la machine une "a-machine" (automatic machine). La machine de Turing peut être définie d'une façon plus mathématique par : Une machine de Turing est un sextuplet (Q,S,G,qo,b,d) : Q : est l'ensemble des états (fini) G : est l'alphabet de travail (fini) b : appartenant à G est un symbole particulier appelé blanc S : est l'alphabet d'entrée (fini) S inclu dans G\b qo : appartenant à Q est l'état initial d : QxG ---> Gx(L,R)xQ est la fonction de transition. A tout couple (état, symbole lu) on associe un triplet (symbole, déplacement (Left ou Right), état) c-machine Dans certains cas, on peut avoir besoin d'une machine à choix ( c-machines ), dont le comportement ne dépend que partiellement de sa configuration lorsqu'une telle machine atteint une configuration ambiguë , un opérateur extérieur doit intervenir et faire un choix arbitraire pour que la machine puisse continuer son travail. Nous aurions besoin de ces machines pour travailler avec des systèmes axiomatiques. Translated by Julien Basch and Patrice Blanchard, in Alan Turing and Jean-Yves Girard, La Machine de Turing, Editions du Seuil, 1995, p. 52-54.

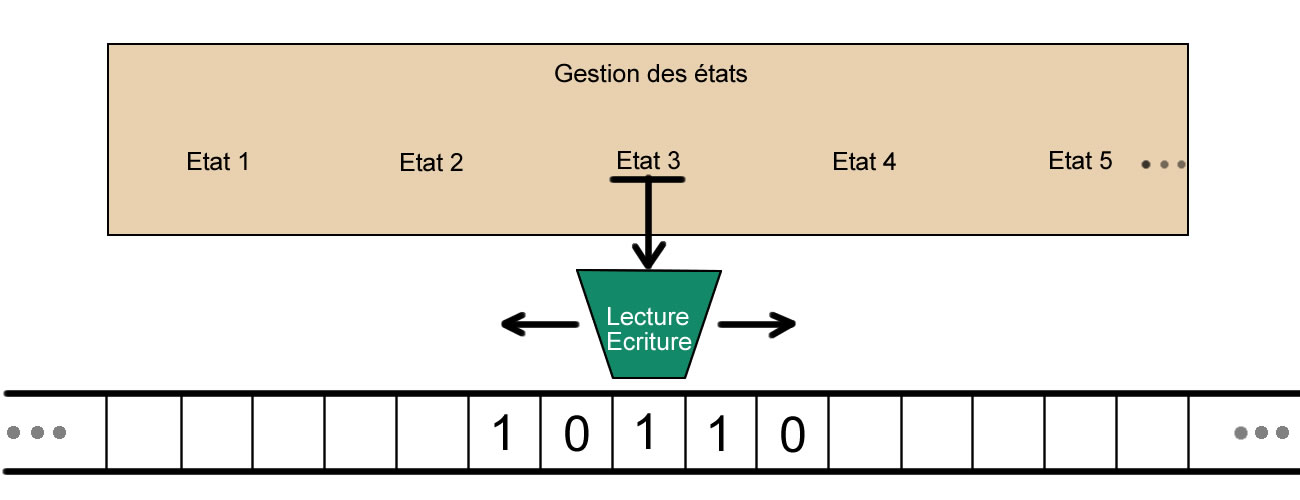Une représentation moderne d'une a-machine avec son ruban et des cases comportant des symboles. La table des transitions donnée par Turing (1936) pour décrire le comportement d'une a-machine construisant la séquence "0101010101...". 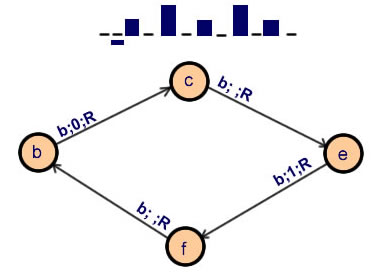Le diagramme de la premiére a-machine décrite par Turing en 1936 pour construire la séquence "0 1 0 1 0 1 0 1 0 1...".