A Programmable Prototype to Build Turing Machines

Home

Alan TURING

History

Turing machine

The actual experimental prototype

Some diagrams of Turing machines for this prototype

Presentations

Presse

Simulator

A new machine

Machines

Ideas

Description

How the machine operates

Technologies

First Turing machine

Easy

Calculations

Sequences

Interesting

Colleges

University

Talks

Videos

Contact

Turing machine description It is a prototype of the machine envisioned by Alan Turing to model the concept of an algorithm and provide a negative answer to the decision problem in first-order logic, posed a few years earlier by Hilbert and Ackermann. Simply put, is it possible to find an “effectively computable” method to decide whether a proposition is provable or not ? This prototype is directly derived from the description he provided in his 1937 paper titled : On computable Numbers, with an Application to the Entscheidungsproblem. This machine is actually the simplest model that can be conceived and satisfies the informal yet universal criteria that characterize an algorithm. It is a universal model of computation, and it can compute anything that any physical computer can compute. Conversely, anything it cannot compute cannot be computed by a computer either. It provides an ideal model for reasoning about the concept of a computation or proof algorithm. a-machine " We may compare a man in the process of computing a real number to a machine which is only capable of a finite number of conditions q1: q2. .... qn; which will be called m-configurations. The machine is supplied with a tape (the analogue of paper) running through it, and divided into sections (called squares) each capable of bearing a symbol. At any moment there is just one square, say the r-th, bearing the symbol T(r) which is "in the machine". We may call this square the scanned square. The symbol on the scanned square may be called the scanned symbol. The "scanned symbol" is the only one of which the machine is, so to speak, "directly aware". However, by altering its m-configuration the machine can effectively remember some of the symbols which it has "seen" (scanned) previously. The possible behaviour of the machine at any moment is determined by the m-configuration qn and the scanned symbol T(r). This pair qr, T(r) will be called the configuration: thus the configuration determines the possible behaviour of the machine. In some of the configurations in which the scanned square is blank (i.e. bears no symbol) the machine writes down a new symbol on the scanned square: in other configurations it erases the scanned symbol. The machine may also change the square which is being scanned, but only by shifting it one place to right or left. In addition to any of these operations the m-configuration may be changed.... If at each stage the motion of a machine is completely determined by the configuration, we shall call the machine an automatic machine (or a-machine)." The Turing machine can be defined in a more mathematical way as : A Turing machine is a sextuple (Q, S, G, qo, b, d). : Q: is the set of states (finite) G: is the working alphabet (finite) b: belonging to G, is a special symbol called blank S: is the input alphabet (finite) S include in G\b qo: belonging to Q, is the initial state d: QxG → Gx(L,R)xQ is the transition function. To every pair (state, symbol read), we associate a triplet (symbol, movement (Left or Right), state).

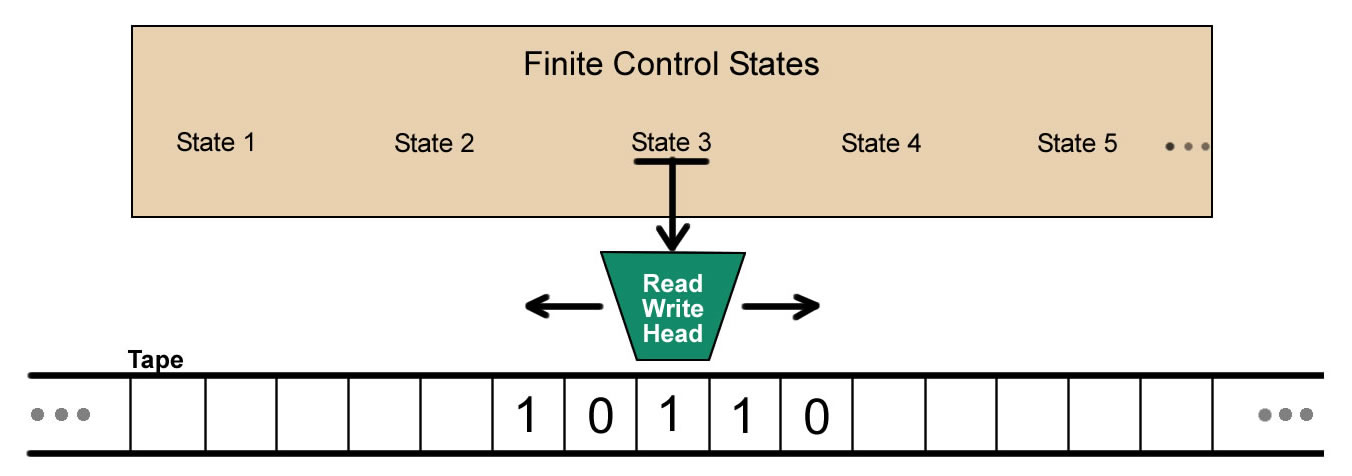A modern representation of an a-machine with its tape and some cells bearing a symbol. The table given by Turing in [Turing36] to describe the behaviour of the a-machine computing the sequence "0101010101...". 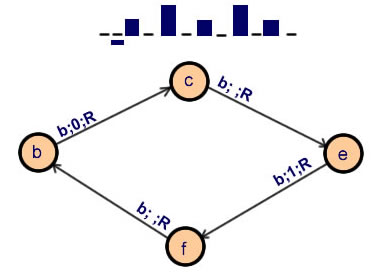The first a-machine described by Turing in 1936 to compute the sequence "0 1 0 1 0 1 0 1 0 1..."