Un peu d'histoire sur le développement des calculateurs et des prémices des ordinateurs modernes.
Machine d'Anticythère (87 av J.C.)
Calculateur analogique
Elle est considérée comme le premier calculateur analogique antique permettant de calculer des positions astronomiques.
C'est un mécanisme de bronze comprenant des dizaines de roues dentées, solidaires et disposées sur plusieurs plans.
Il est garni de nombreuses inscriptions grecques.
Sources :
|
|
Le fragment principal de la machine d'Anticythère : 20 à 20 cm environ
|
Le boulier
Calculateur manuel
ELes bouliers permettent d'effectuer le calcul des opérations élémentaires : additions, soustractions, multiplications et divisions.
Dans des mains expertes, il est cependant possible de réaliser d'autres opérations comme le calcul de racines éniémes ou la conversion entre différentes bases.
Le boulier est lié au système de numération décimale, mais il existe deux grandes catégories de bouliers.
Les bouliers en base 10, pour lesquels chaque boule représente, selon la tige sur laquelle elle se trouve, une unité, une dizaine, une centaine.
Ces bouliers se rencontrent essentiellement en Europe occidentale et de l'Est. Les décimales peuvent aussi être représentées sur la première tige.
Et les bouliers en base alternée (5, 2) pour lesquels chaque tige comprend deux parties :
une partie supérieure sur laquelle les boules valent 5 unités (ou 5 dizaines, 5 centainesé selon la position de la tige) et une partie inférieure sur
laquelle les boules valent 1 unité (ou 1 dizaine, 1 centaineé selon la position de la tige). Ces bouliers se rencontrent essentiellement en Asie.
Sources :
|
|
|
Blaise PASCAL (1623-1662)
Machine à calculer conçue en 1642 :
 |
Elle permettait d'additionner et de soustraire deux nombres d'une façon directe et de faire des multiplications et des divisions par répétitions.
Sources :
|
|
Une pascaline, signée par Pascal en 1652, visible au musée des arts et métiers à Paris.
|
Gottfried Wihelm LEIBNIZ (1646-1716)
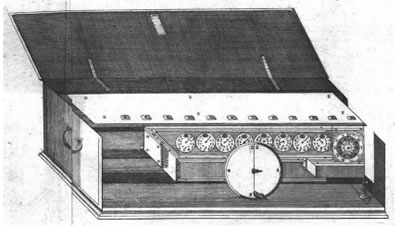
Machine présentée à la Société Royale de Londres en 1673 :
Traduction du texte de Leibniz par Madame Colette Chantal Adam
|
Leibniz décrit dans ce texte sa machine arithmétique, sur laquelle il travaillait dès sa jeunesse, et qui permet de faire les multiplications en
décalant une partie mobile d'un cran vers la gauche, comme lorsqu'on pose une multiplication à la main..
Leibniz a rêvé d'une logique qui serait calcul algorithmique et donc mécaniquement décidable (calculus ratiocinator).
Leibniz annonce ainsi la langue artificielle et purement formelle développée par Frege.
Il fut le premier à envisager la numération binaire Voir
Sources :
|
|
|
|
Willgodt Theophil ODHNER (1845 - 1905)
Arithmomètre d'Odhner inventé en Russie en 1873 :
Odhner eu l'idée de sa machine alors qu'il réparait un arithmomètre en 1871 (L'Arithmomètre était le seul calculateur mécanique commercialisé à l'époque).
Il décida de remplacer les cylindres de Leibniz qui rendaient la machine lourde et encombrante, par des roues à nombre variable de dents, qui étaient
plus légères et beaucoup plus compactes. En gardant le même mode opératoire, il en assura un succès immédiat.
Odhner finit son premier prototype en 1873. En 1876 il construit 14 machines pour Ludvig Nobel, son employeur d'alors, qu'il finira en 1877.
Il dépose des brevets d'invention en Europe et aux états-Unis entre 1878-1879 et un nouveau brevet en 1890. Il commence la production industrielle
de son Arithmomètre en 1890.
Sources :
|
A luxury mechanical calculator presented to Swedish king Gustaf V by Wilgodt Odhner. TM22900. Photo:Archive of National Museum of Science and Technology.
|
Charles BABBAGE (1791-1871)
La machine analytique
Une avancée fondamentale en matière d'automatisation des calculs fut réalisée par Charles Babbage entre 1834 et 1836.
Il y définit les principaux concepts sur lesquels reposent les machines informatiques, soit :
- un dispositif d'entrée avec deux lecteurs de cartes perforées (programmes et données)
- un organe de commande gérant le transfert des nombres et leur mise en ordre pour le traitement
- un magasin permettant de stocker les résultats intermédiaires ou finaux
- un moulin chargé d'exécuter les opérations sur les nombres
- trois types d'imprimantes
La machine à différences
Il présente un modèle de sa machine à différences à la Société royale d'astronomie en 1821.
Le but de la machine est de calculer les polynômes en utilisant une méthode de calcul dite méthode différentielle.
Entre 1847 et 1849, il dessina les plans de la machine à différences no 2.
Cette nouvelle machine requêrait 3 fois moins de pièces que la machine à différences no 1, tout en offrant une puissance de calcul équivalente.
Babbage n'essaya jamais de la construire.
En 1985, le musée des sciences de Londres entreprit de construire un exemplaire de la machine à différences no 2, afin de célébrer le 200e anniversaire
de Babbage en 1991. Le module de calcul fut terminé à temps en 1991, et c'est finalement en 2002 que la machine fut totalement achevée avec son module
d'impression et de stéréotype.
Construite en respectant scrupuleusement les plans originaux, elle est composée de 8 000 pièces, pèse 5 tonnes, mesure 3 mètres de large,
2 mètres de haut et 45 cm de profondeur. Cet exemplaire est aujourd'hui exposé au musée des sciences de Londres.
Sources :
|
Prototype (1871) non terminé de la machine analytique de Babbage, exposée au Science Museum de Londres.
Une partie de la machine à différences de Babbage.
|
IBM initialement nomme CTR
L'entreprise Computing-Tabulating-Recording Company, le précurseur d'IBM, est fondée le 16 juin 1911.
Utilisation de cartes perforées
- Analyses statistiques
- Recensement des populations
Sources : IBM Tabulators and Accounting Machines
la Compagnie des machines Bull (CMB), française, est fondée en 1930
Sources : Tabulatrice T30 - 1932 - Egli.Bull
|
|
|
Alan Turing (1912-1954)
a-machine
"Nous pouvons comparer un homme en train de calculer un nombre réel à une machine qui ne peut prendre qu'un nombre fini d'tats q1: q2. Qn ....;
qui seront appelé "m-configurations".
La machine comporte un "ruban" (l'analogue de papier) qui la traverse, divisé en sections (appelé "carrés") dans lesquels on peut inscrire un "symbole".
A tout moment, un seul carré peut se trouver "dans la machine" on nomme T(r) le symbole qu'il porte. Ce carré est le "carré traité" et le symbole qu'il porte, le "symbole traité".
Le symbole traité est le seul dont la machine est pour ainsi dire "directement consciente". Cependant, en changeant d'état-m, la machine peut se souvenir de certains des
symboles qu'elle a vus (balayés) avant.
A tout instant, le comportement de la machine est déterminé par la m-configuration qn et le symbole lu T(r).
Cette paire de qr, T(r) sera appelé la "configuration", cette configuration détermine le comportement de la machine. Selon les cas, la machine pourra écrire
un symbole dans un carré vierge (blank), effacer un symbole déjà écrit dans un carré, ou bien la machine pourra changer de carré par un déplacement
d'une case à gauche ou à droite. De plus, la m-configuration peut être changée.
Si à chaque étape, le comportement de la machine est complètement déterminé par sa configuration, nous appelerons la machine une "a-machine" (automatic machine).
Extract of On computable numbers...[Turing 1936]
Référence pour la traduction : "Alan Turing : l'homme qui inventa l'informatique" de David Leavitt aux éditions DUNOD.
|
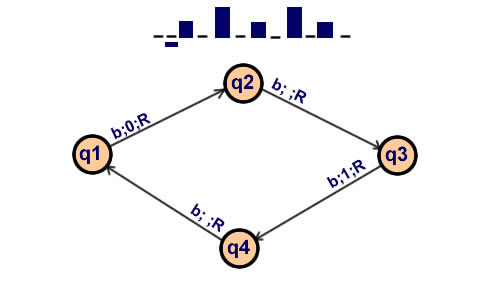Le diagramme de la première a-machine
décrite par Turing en 1936 pour construire la séquence "0 1 0 1 0 1 0 1 0 1...".
|
Curt Herzstark (1902-1988)
Curt Herzstark est arrêté en 1943 par les nazis et il est interné au camp de Buchenwald. Son expertise technique lui évite le pire et il peut travailler aux plans de sa calculatrice la "Curta".
La Curta est une petite calculatrice mécanique produite entre 1948 et 1972 par Contina AG Mauren au Liechtenstein.
Elle est composée d'un corps cylindrique et d'une petite manivelle la faisant ressembler à un moulin à poivre ou à café.
Cette toute petite machine permet d'effectuer très rapidement les quatre opérations arithmétiques de base et, après apprentissage, d'autres opérations comme les racines carrées.
Voir sur Wikipedia :
Curt Herzstark or La calculatrice Curta.
|
|
von Neumann (1903-1957)
Architecture de von Neumann
Von Neumann a donné son nom à l'architecture de von Neumann utilisée dans la quasi totalité des ordinateurs modernes, l'apport d'autres
collaborateurs de l'EDVAC en est par conséquent grandement minimisé (on citera J. Presper Eckert et John William Mauchly parmi d'autres).
Cela est dû au fait qu'il est, en 1945, le rapporteur des travaux pionniers en la matiére (First Draft of a Report on the EDVAC).
Le modèle de calculateur à programme auquel son nom reste attaché et qu'il attribuait lui-même à Alan Turing, possède une unique mémoire
qui sert à conserver les logiciels et les données. Ce modèle, extrêmement innovant pour l'époque, est à la base de la conception de nombre d'ordinateurs.
L'architecture de von Neumann décompose l'ordinateur en 4 parties distinctes :
- l'unité arithmétique et logique (UAL) ou unité de traitement, qui effectue les opérations de base
- l'unité de contrôle, qui est chargée du séquençage des opérations
- la mémoire, qui contient à la fois les données et le programme qui indique à l'unité de contrôle quels calculs faire sur ces données.
La mémoire se divise en mémoire vive (programmes et données en cours de fonctionnement) et mémoire de masse (programmes et données de base de la machine);
- les dispositifs d'entrée-sortie, qui permettent de communiquer avec le monde extérieur
Sources :
|
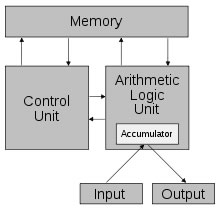Schéma de l'architecture de von Neumann
|
