A Programmable Prototype to Build Turing Machines

Home Alan TURING History Turing machine The actual experimental prototype Some diagrams of Turing machines for this prototype Presentations Presse Simulator A new
machine
Machines Ideas Description How the machine operates Technologies First Turing machine Easy Calculations Sequences Interesting Colleges University Talks Videos Contact

A little history on the development of computers and the beginnings of modern computers.

The abacus

Manual calculator


Abacuses allow for the calculation of basic operations: addition, subtraction, multiplication, and division.
In expert hands, however, it is possible to perform other operations, such as calculating nth roots or converting between different bases.


The abacus is linked to the decimal numeral system, but there are two main categories of abacuses.

Abacuses in base 10, where each bead represents a unit, a ten, or a hundred, depending on the rod it is on. These abacuses are mainly found in Western and Eastern Europe.



Sources :
 
Blaise PASCAL (1623-1662)

Calculating machine conceived in 1642 :

It possible to add and subtract two numbers in a direct way and make multiplication and division by repetitions.


Sources :


A pascaline signed by Pascal in 1652, visible at the Museum of Arts and Crafts in Paris.
 


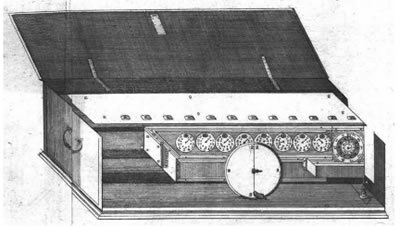
Gottfried Wihelm LEIBNIZ (1646-1716)

Machine presented to the Royal Society of London in 1673 :

This machine consists of a fixed part and a movable part.
This device allows the movable part to shift to the left depending on the power of ten of the multiplier being considered.
For example, to multiply by 35, we start by multiplying by 5, then shift the multiplier one step to the left and multiply by 3.

 


Willgodt Theophil ODHNER (1845 - 1905)

Arithmometer of Odhner invented in Russia in 1873 :

Odhner got the idea for his machine while repairing an arithmometer in 1871 (the Arithmometer was the only commercially available mechanical calculator at the time). He decided to replace Leibniz's cylinders, which made the machine heavy and bulky, with variable-tooth wheels that were lighter and much more compact. By maintaining the same operating method, he ensured its immediate success.
Odhner completed his first prototype in 1873. In 1876, he built 14 machines for Ludvig Nobel, his employer at the time. He filed invention patents in Europe and the United States between 1878 and 1879, and a new patent in 1890. He began the industrial production of his Arithmometer in 1890.

Sources :


A luxury mechanical calculator presented to Swedish king Gustaf V by Wilgodt Odhner. TM22900. Photo:Archive of National Museum of Science and Technology.
 


Charles BABBAGE (1791-1871)

Difference engine

A fundamental breakthrough in the automation of calculations was made by Charles Babbage between 1834 and 1836. Babbage began in 1822 with what he called the difference engine, made to compute values of polynomial functions. It was created to calculate a series of values automatically. By using the method of finite differences, it was possible to avoid the need for multiplication and division. Some parts of the prototype survive in the Museum of the History of Science, Oxford.[137] This prototype evolved into the "first difference engine." It remained unfinished and the finished portion is located at the Science Museum in London. This first difference engine would have been composed of around 25,000 parts, weigh fifteen tons (13,600 kg), and would have been 8 ft (2.4 m) tall.

Analytical engine

The major innovation was that the Analytical Engine was to be programmed using punched cards: the Engine was intended to use loops of Jacquard's punched cards to control a mechanical calculator, which could use as input the results of preceding computations. The machine was also intended to employ several features subsequently used in modern computers, including sequential control, branching and looping. It would have been the first mechanical device to be, in principle, Turing-complete. The Engine was not a single physical machine, but rather a succession of designs that Babbage tinkered with until his death in 1871.

Babbage had no research team. Ada Lovelace corresponded with him during his development of the Analytical Engine. She is credited with developing an algorithm for the Analytical Engine to calculate a sequence of Bernoulli numbers. Although there is disagreement over how much of the ideas were Lovelace's own, she is often described as the first computer programmer.


Completed models

The London Science Museum has constructed two Difference Engines according to Babbage's plans
Sources :


Unfinished prototype (1871) of Babbage's analytical engine, on display in the Science Museum, London.

Part of Charles Babbage's difference engine, assembled after his death by his son, Henry Prevost Babbage (1824-1918), using parts found in Charles' laboratory.
 


Alan Turing (1912-1954)

a-machine

" We may compare a man in the process of computing a real number to a machine which is only capable of a finite number of conditions q1: q2. .... qn; which will be called " m-configurations ".
The machine is supplied with a "tape" (the analogue of paper) running through it, and divided into sections (called "squares") each capable of bearing a "symbol".
At any moment there is just one square, say the r-th, bearing the symbol T(r) which is "in the machine". We may call this square the "scanned square". The symbol on the scanned square may be called the " scanned symbol". The "scanned symbol" is the only one of which the machine is, so to speak, "directly aware".
However, by altering its m-configuration the machine can effectively remember some of the symbols which it has "seen" (scanned) previously. The possible behaviour of the machine at any moment is determined by the m-configuration qn and the scanned symbol T(r).
This pair qr, T(r) will be called the '' configuration'': thus the configuration determines the possible behaviour of the machine. In some of the configurations in which the scanned square is blank (i.e. bears no symbol) the machine writes down a new symbol on the scanned square: in other configurations it erases the scanned symbol.
The machine may also change the square which is being scanned, but only by shifting it one place to right or left. In addition to any of these operations the m-configuration may be changed....
If at each stage the motion of a machine is completely determined by the configuration, we shall call the machine an "automatic machine" (or a-machine)."
Extract of On computable numbers...[Turing 1936]


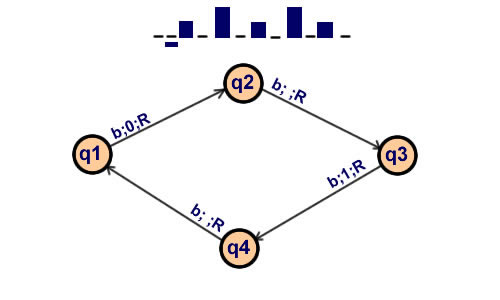The first a-machine described by Turing in 1936 to compute the sequence "0 1 0 1 0 1 0 1 0 1...".
 


Curt Herzstark (1902-1988)


Curt Herzstark was arrested in 1943 by the Nazis and interned in the Buchenwald camp. His technical expertise saves him the worst and he can work on plans for his "Curta" calculator.

The Curta is a small mechanical calculator produced between 1948 and 1972 by Contina AG Mauren in Liechtenstein.
It is composed of a cylindrical body and a small crank making it look like a pepper or coffee grinder.
This very small machine makes it possible to carry out very quickly the four basic arithmetic operations and, after learning, other operations such as square roots.

View :       Curt Herzstark       or       La calculatrice Curta      on Wikipedia.


 


von Neumann (1903-1957)

Architecture de von Neumann

The earliest computing machines had fixed programs.
Changing the program of a fixed-program machine requires re-wiring, re-structuring, or re-designing the machine. With the proposal of the stored-program computer, this changed. Such a computer can store a set of instructions (a program) in memory that details the calculation.

The term Von Neumann architecture, also known as the Von Neumann model or the Princeton architecture, derives from a 1945 computer architecture description by the mathematician and physicist John von Neumann and others, First Draft of a Report on the EDVAC.

This describes a design architecture for an electronic digital computer with subdivisions of a processing unit consisting of 4 parts:
  1. an arithmetic logic unit and processor registers; (UAL) ou unité de traitement, qui effectue les opérations de base;
  2. a control unit containing an instruction register and program counter;
  3. a memory to store both data and instructions;
  4. external mass storage, and input and output mechanisms.

Sources :


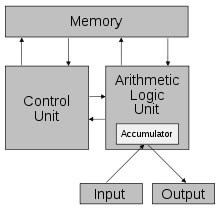Von Neumann architecture scheme