|
Un prototype programmable pour concrétiser la machine de Turing | |
| Accueil | Alan TURING | Histoire | Machine de Turing | Le prototype expérimental réalisé | Quelques diagrammes de machines de Turing pour ce prototype | Interventions | Presse | Simulateur | Nouvelle machine |
|||||||||
| Machines | Idées | Descriptif | Fonctionnement | Technologie | 1ère machine de Turing | Facile | Calculateurs | Suites | Intéressant | Lycées | Universités | Conférences | Vidéos | Contact | ||||
| Déplacements de la tête de lecture/écriture | |||||
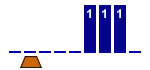
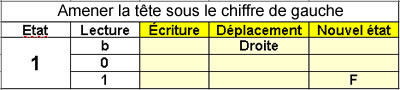
| Déplacer la tête sous le chiffre de gauche 1 état |
 |
 |
 |
 |
 |
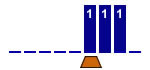
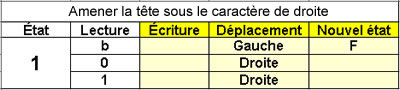
| Déplacer la tête sous le chiffre de droite 1 état |
|
 |
 |
 |
 |
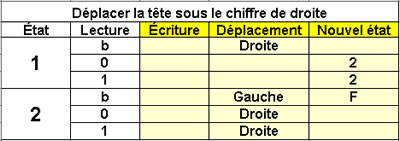
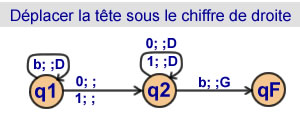
| Déplacer la tête sous le chiffre de droite 2 états |
|
 |
 |
 |
 |
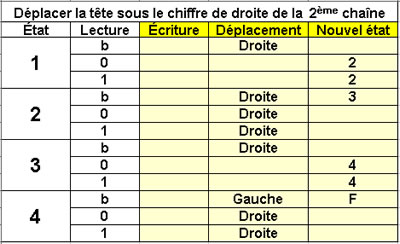
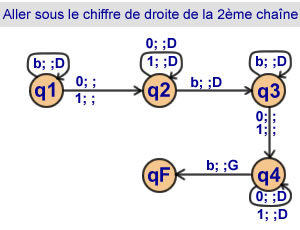
| Déplacer la tête sous le chiffre de droite de la deuxième chaîne 4 états |
|
 |
 |
 |
 |
| Les chaînes de caractères | |||||
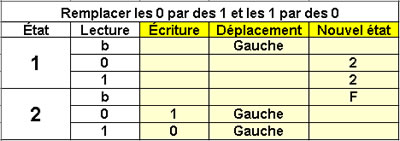
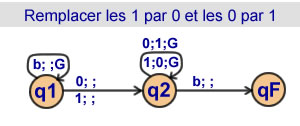
| Trouver la séquence remplacer les 0 par des 1 et remplacer les 1 par des 0 2 états |
|
 |
 |
 |
 |
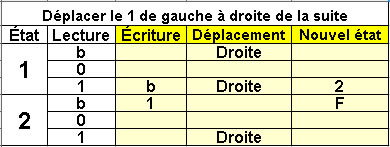
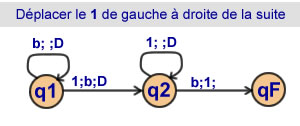
| Déplacer une suite de 1 Le 1 de gauche sera déplacé à droite de la suite 2 états |
|
 |
 |
 |
 |
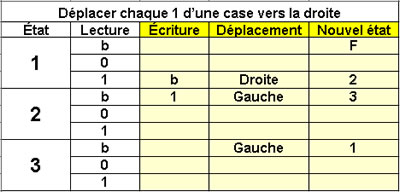
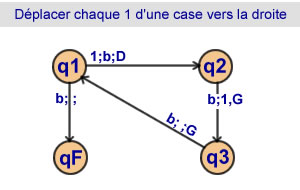
| Déplacer une suite de 1 Chaque 1 sera déplacé d'une case vers la droite 3 états |
|
 |
 |
 |
 |
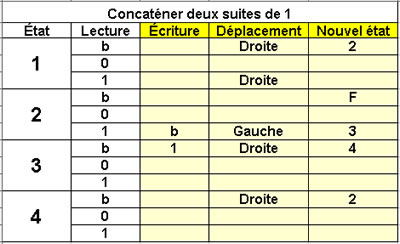
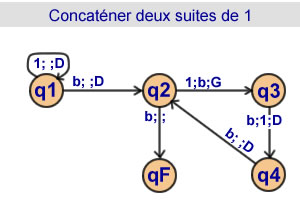
| Concaténer deux suites de 1 4 états |
|
 |
 |
 |
 |
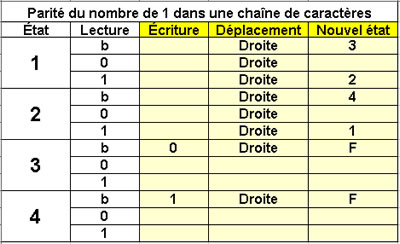
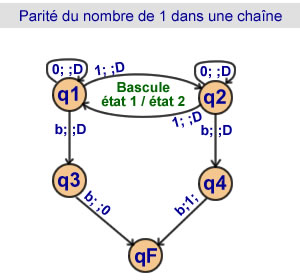
| Parité du nombre de 1 dans une chaîne de caractères 4 états La téte parcours la chaîne et passe de l'état 1 à l'état 2 et inversement à chaque fois qu'elle lit un 1. Selon qu'elle termine à l'état 1 ou à l'état 2 le nombre de 1 est pair ou impair. |
|
 |
 |
 |
 |
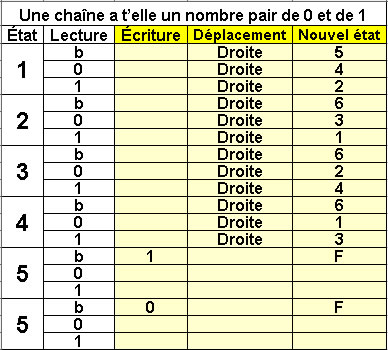
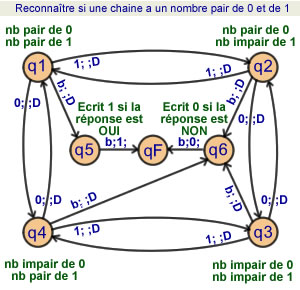
| Déterminer s'il y a un nombre pair de 0 et un nombre pair de 1 dans une chaîne de caractères 6 états |  |
 |
 |
 |
|
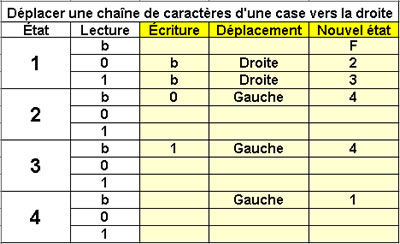
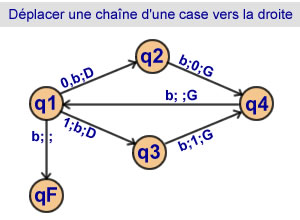
| Déplacer une chaîne de caractères d'une case vers la droite 4 états |
|
 |
 |
 |
 |
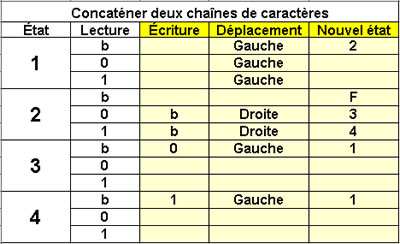
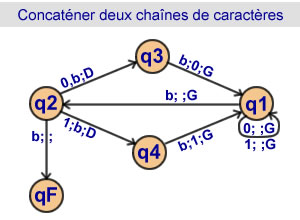
| Concaténer deux chaînes de caractères 4 états L'état 1 amène la tête de lecture/écriture sous le caractères de droite de la première chaîne. |
|
 |
 |
 |
 |
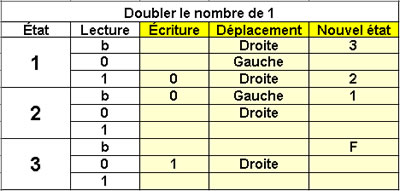
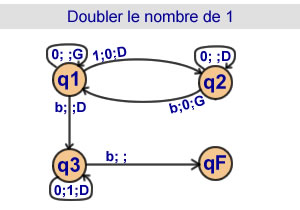
| Doubler le nombre d'élémentsd'une suite de 1 3 états |
|
 |
 |
 |
 |
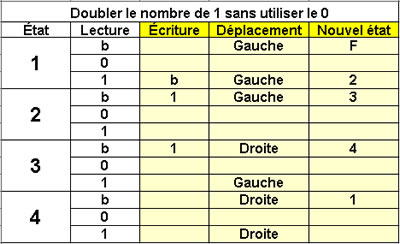
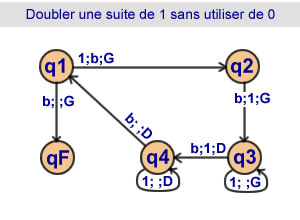
| Doubler une suite de 1 sans utiliser de 0 4 états |
|
 |
 |
 |
 |
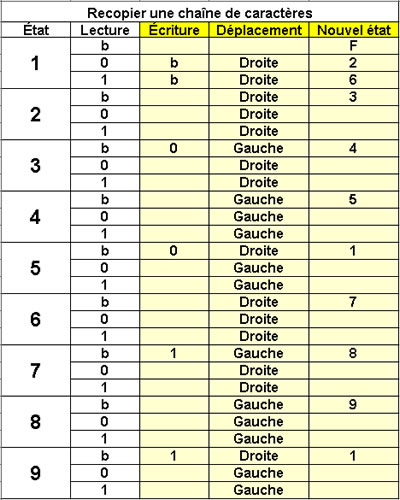
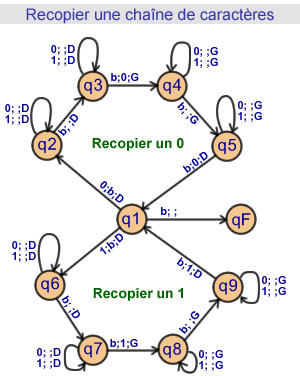
| Recopier une chaîne de caractères 9 états |
|
 |
 |
 |
 |
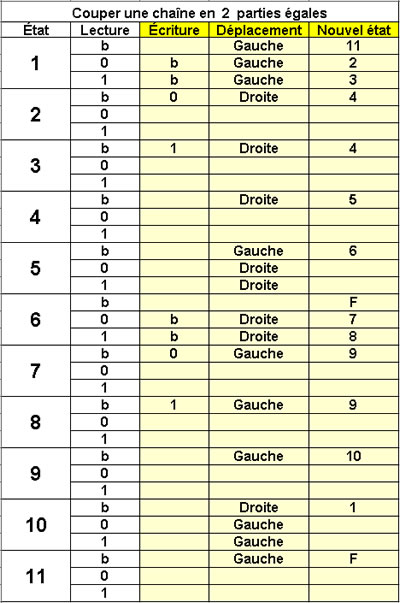
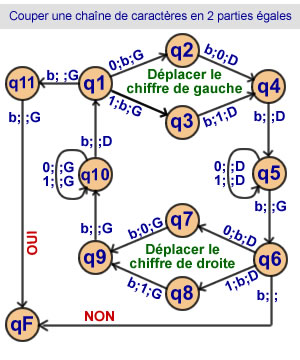
| Couper une chaîne de caractères en deux parties égales 11 états Si la chaîne n'a pas un nombre pair de caractères l'algorithme s'arrête à l'état 6. |
|
 |
 |
 |
 |
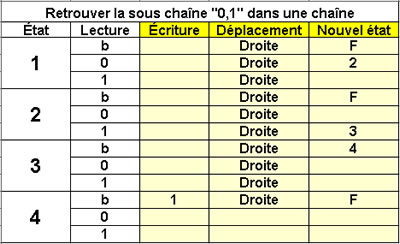
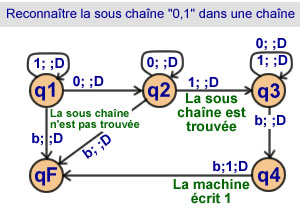
| Retrouver la sous chaîne "0,1" dans une chaîne 4 états |
|
 |
 |
 |
 |
| Les premiers calculs | |||||
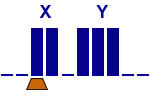
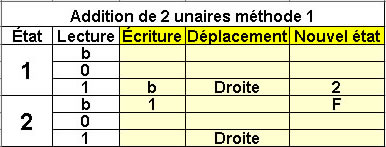
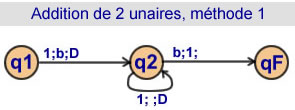
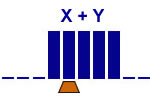
| Addition de 2 unaires Solution 1 2 états |
|
 |
 |
 |
 |
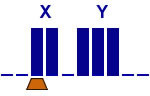
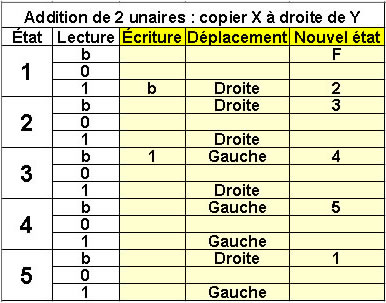
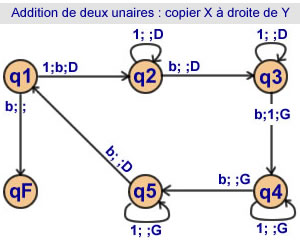
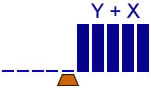
| Addition de 2 unaires Solution 2 Ajouter X à droite de Y 5 états |
|
 |
 |
 |
 |
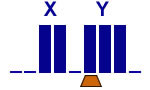
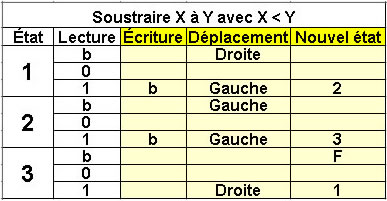
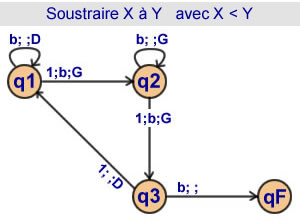
| Soustraire X à Y écrits en unaire Avec X < Y 3 états |
|
 |
 |
 |
 |
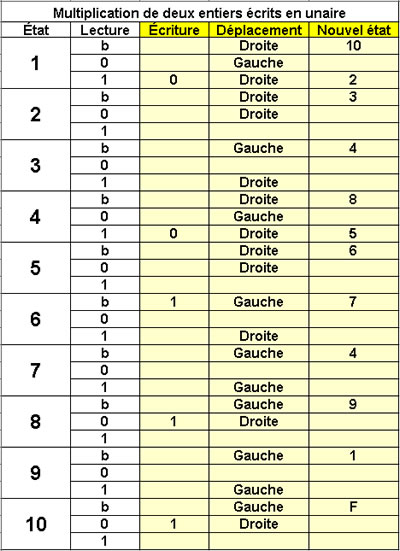
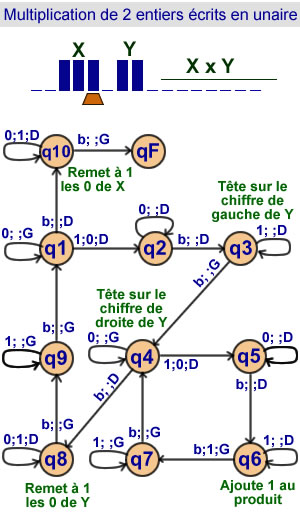
| Multiplication de deux entiers écrits en unaire 10 états |
|
 |
 |
 |
 |
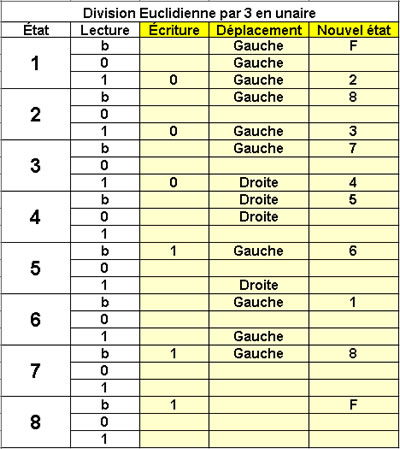
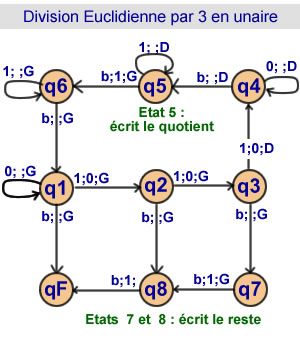
| Division Euclidienne par 3 en unaire 8 états |
|
 |
 |
 |
 |
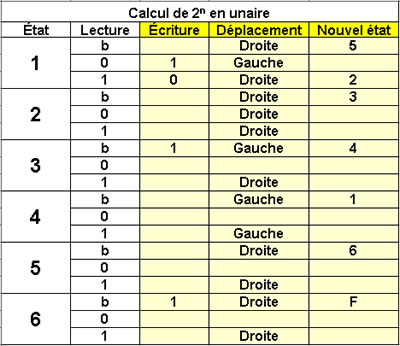
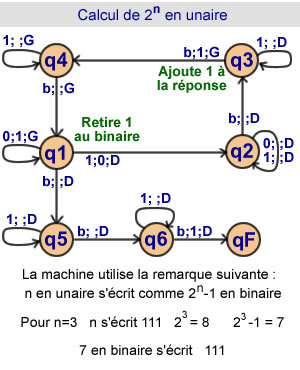
| Calcul de 2n en unaire
La machine traite l'unaire comme le binaire auquel il faudra ajouter 1 pour obtenir 2n 6 états |
|
 |
 |
 |
 |
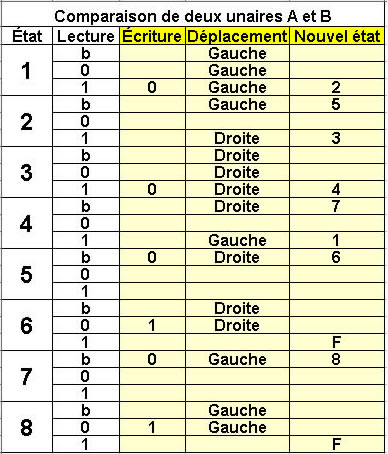
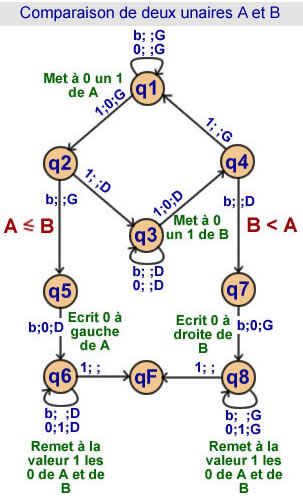
| Comparaison de deux unaires 8 états |
 |
 |
 |
 |
|
| Premiers calculs avec des nombres binaires | |||||
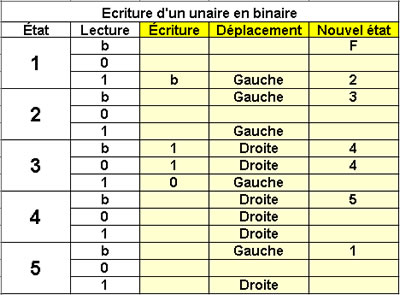
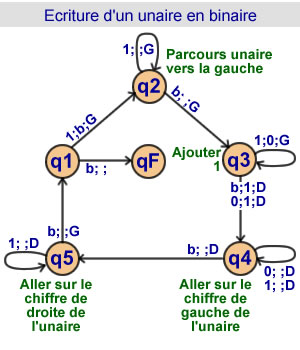
| Ecriture d'un unaire en binaire 5 états |
|
 |
 |
 |
 |
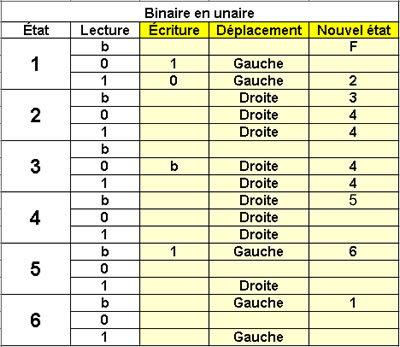
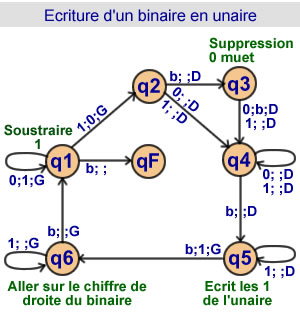
| Ecriture d'un binaire en unaire 6 états |
|
 |
 |
 |
 |
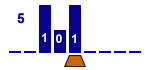
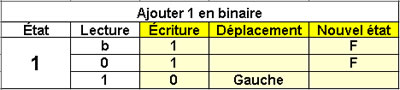
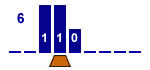
| Ajouter 1 à un nombre binaire 1 état |
|
 |
 |
 |
 |
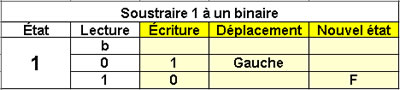
| Soustraire 1 à un binaire 1 état Le binaire > 1 |
|
 |
 |
 |
 |
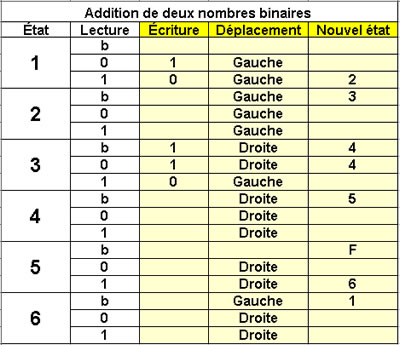
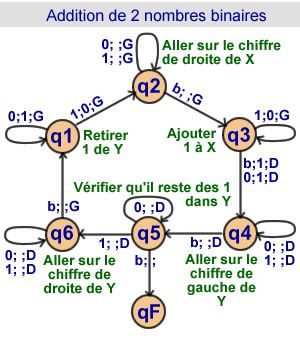
| Addition de deux nombres binaires 6 états |
|
 |
 |
 |
 |
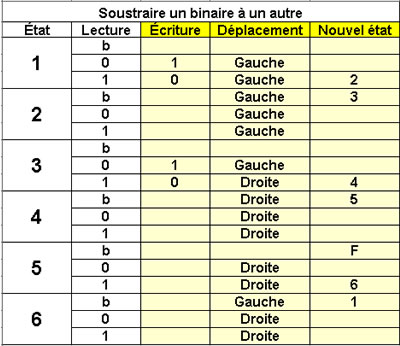
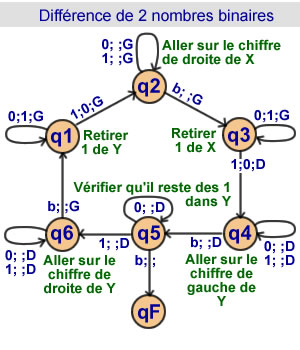
| Soustraire un binaire à un autre 6 états On suppose X > Y > 0 |
|
 |
 |
 |
 |
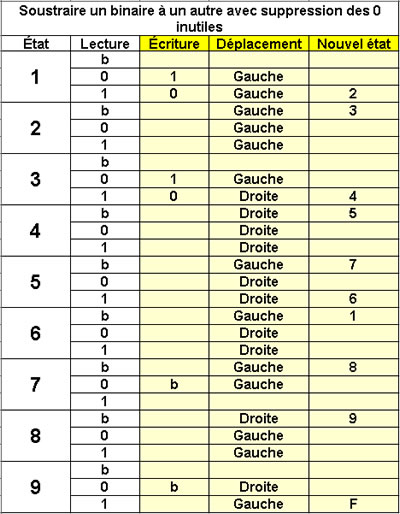
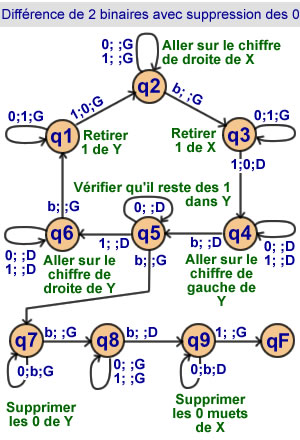
| Soustraire un binaire à un autre avec suppression des 0 inutiles 9 états On suppose X > Y > 0 |
|
 |
 |
 |
 |