|
A Programmable Prototype to Build Turing Machines | |
| Home | Alan TURING | History | Turing machine | The actual experimental prototype | Some diagrams of Turing machines for this prototype | Presentations | Presse | Simulator | A new machine |
|||||||||
| Machines | Ideas | Description | How the machine operates | Technologies | First Turing machine | Easy | Calculations | Sequences | Interesting | Colleges | University | Talks | Videos | Contact | ||||
| Read/write head movements | |||||
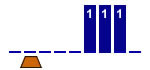
| Place the head under the left digit of the string 1 state |
 |
 |
 |
 |
 |
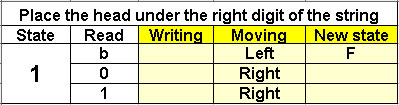
| Place the head under the right digit of the string 1 state |
|
 |
 |
 |
 |
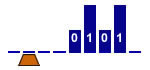
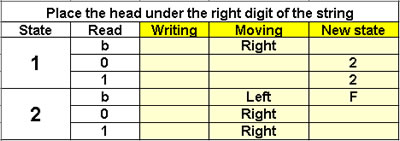
| Place the head under the right digit of the string 2 states |
|
 |
 |
 |
 |
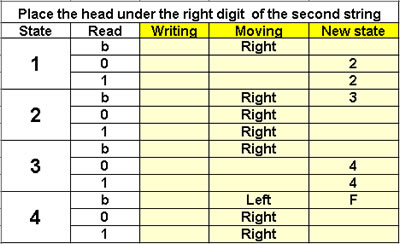
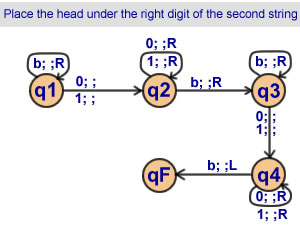
| Place the head under the right digit of the second string 4 states |
|
 |
 |
 |
 |
| Character strings | |||||
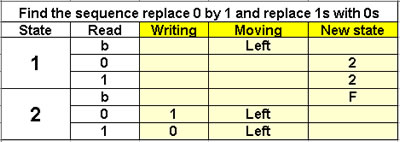
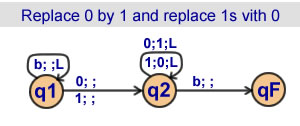
| Find the sequence replace 0 by 1 and replace 1s with 0s 2 states |
|
 |
 |
 |
 |
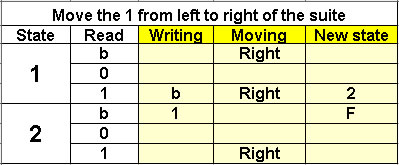
| Move the 1 from left to right of the suite 2 states |
|
 |
 |
 |
 |
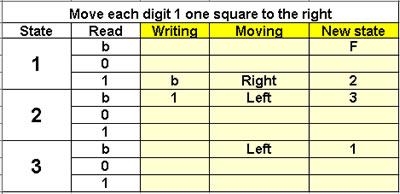
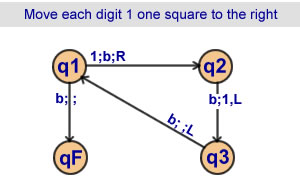
| Move each digit 1 one square to the right 3 states |
|
 |
 |
 |
 |
| Concatenate two sequences of 1 4 states |
|
 |
 |
 |
 |
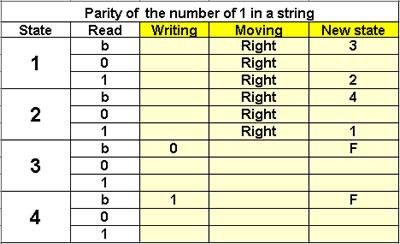
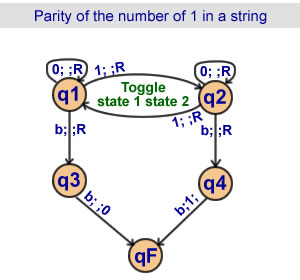
| Parity of the number of 1 in a string 4 states The head goes through the chain and goes from state 1 to state 2 and vice versa each time it reads a 1. Depending on whether it ends in state 1 or in state 2, the number of 1 is even or odd. |
|
 |
 |
 |
 |
| Determining if a chain has an even number of 0's and 1's 6 states | |
 |
 |
 |
 |
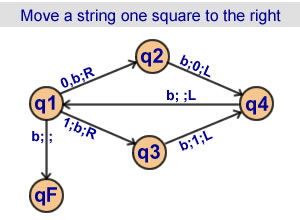
| Move a string one square to the right 4 states |
|
 |
 |
 |
 |
| Concatenate two strings 4 states State 1 brings the head of read / write under the characters right of the first string.. |
|
 |
 |
 |
 |
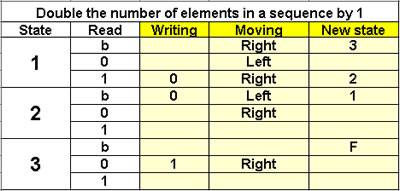
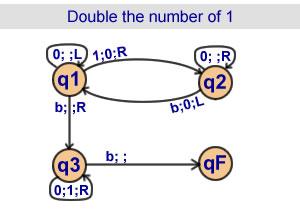
| Double the number of elements in a sequence by 1 3 states |
|
 |
 |
 |
 |
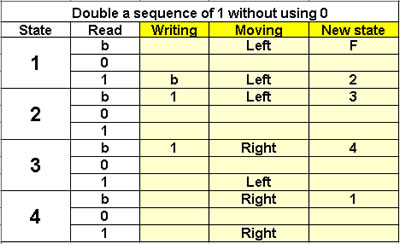
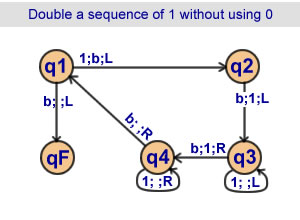
| Double a sequence of 1 without using 0 4 states |
|
 |
 |
 |
 |
| Copy a string 9 states |
|
 |
 |
 |
 |
| Cut a string in two equal parts 11 states String has an even number of characters. |
|
 |
 |
 |
 |
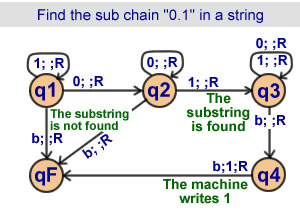
| Find the sub chain "0.1" in a string 4 states |
|
 |
 |
 |
 |
| The first calculations | |||||
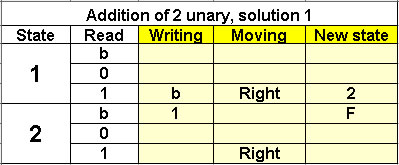
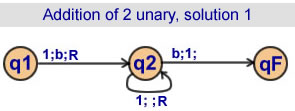
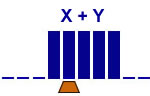
| Addition of 2 unaries Solution 1 2 states |
|
 |
 |
 |
 |
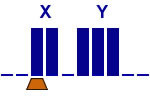
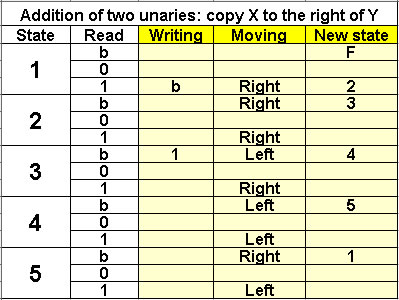
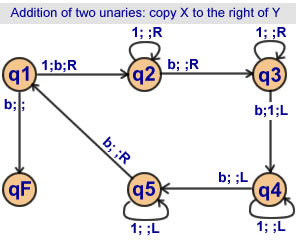
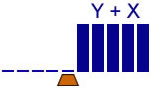
| Addition of 2 unaries Solution 2 Copy X to the right of Y 5 states |
|
 |
 |
 |
 |
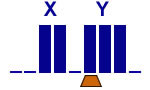
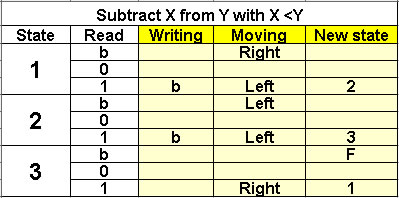
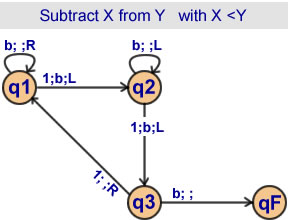
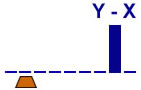
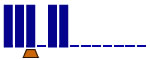
| Subtract X from Y with X < Y 3 states |
|
 |
 |
 |
 |
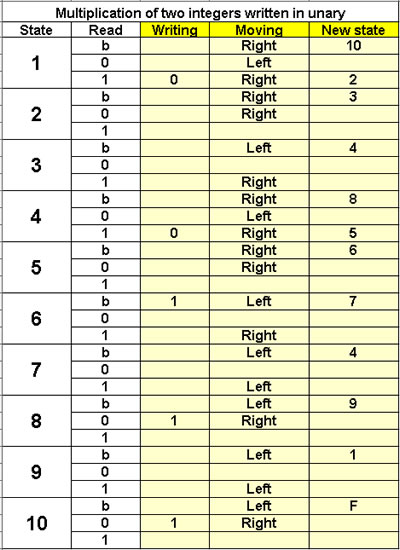
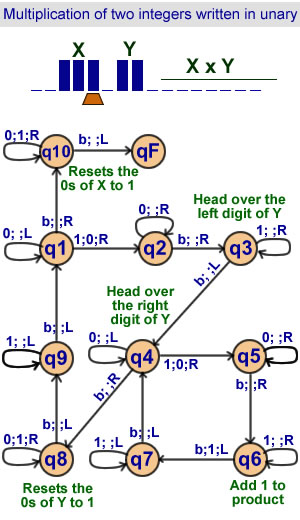
| Multiplication of two integers written in unary 10 states |
|
 |
 |
 |
 |
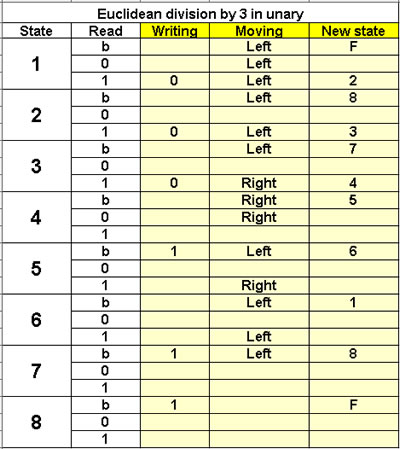
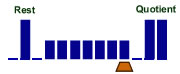
| Euclidean division by 3 in unary 8 states |
|
 |
 |
 |
 |
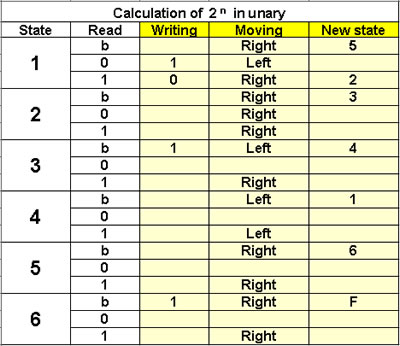
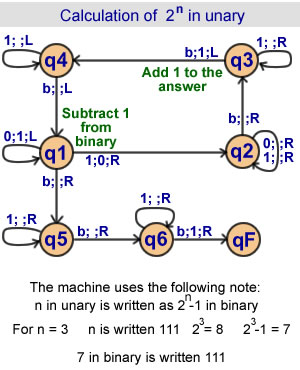
| Calculation of 2 n in unary
The machine treats the unary as the binary to which it will add 1 to obtain 2 n 6 states |
|
 |
 |
 |
 |
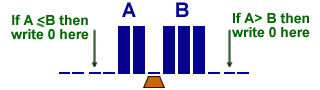
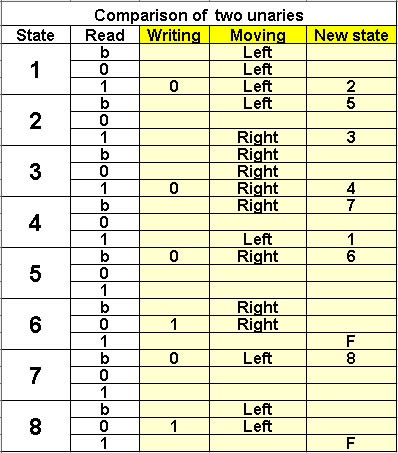
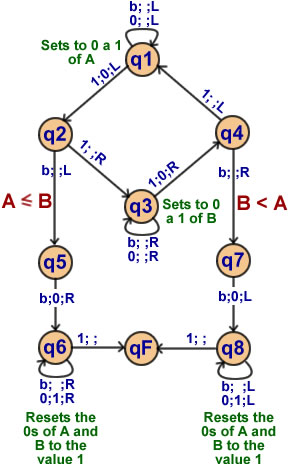
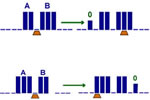
| Comparison of two unaries 8 states |
 |
 |
 |
 |
|
| First calculations with binary numbers | |||||
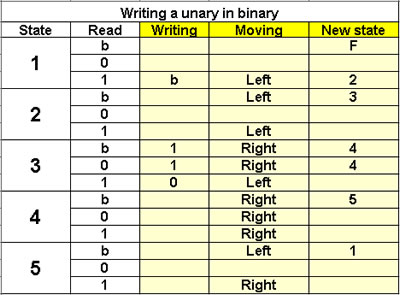
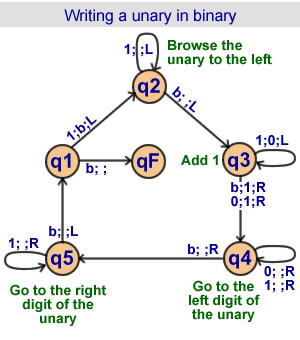
| Writing a unary in binary 5 states |
|
 |
 |
 |
 |
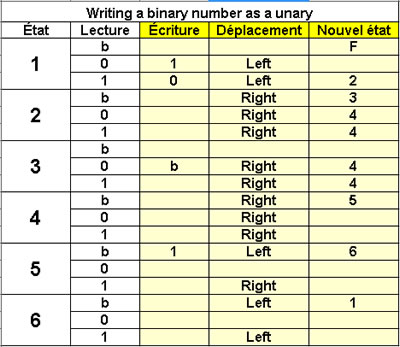
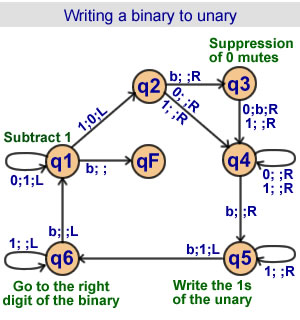
| Writing a binary to unary 6 states |
|
 |
 |
 |
 |
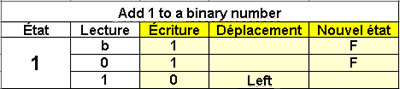
| Add 1 to a binary number 1 state |
|
 |
 |
 |
 |
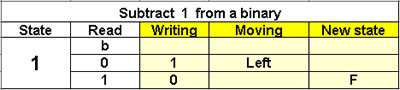
| Subtract 1 from a binary 1 state The binary is > 1 |
|
 |
 |
 |
 |
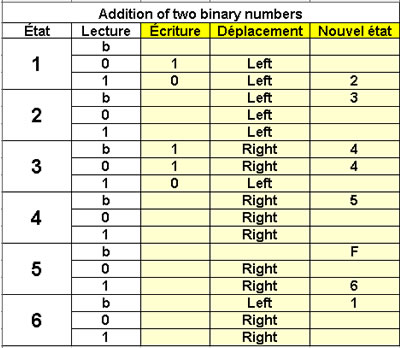
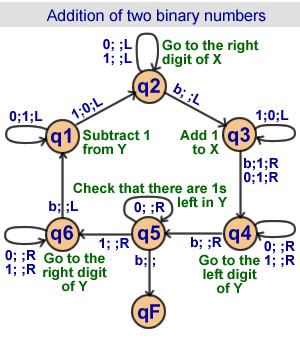
| Addition of 2 binary numbers 6 states |
|
 |
 |
 |
 |
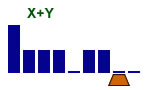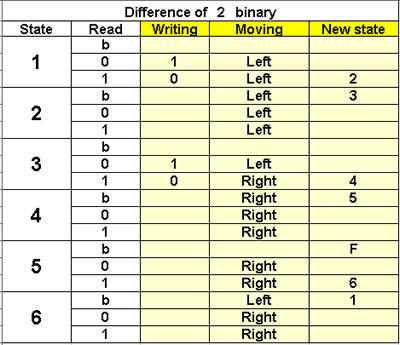
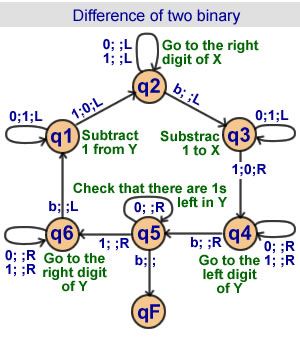
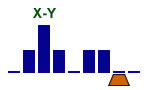
| Subtract one binary from another 6 states We assume X > Y > 0 |
|
 |
 |
 |
 |
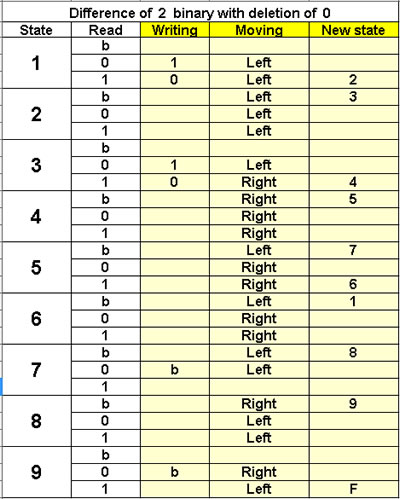
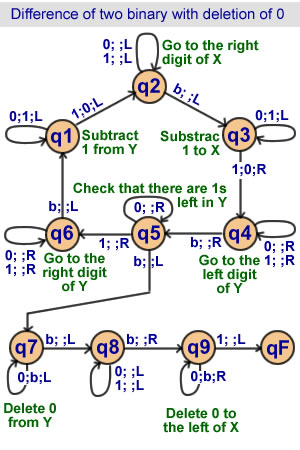
| Difference of 2 binary with deletion of 0 9 states We assume X > Y > 0 |
|
 |
 |
 |
 |