|
A Programmable Prototype to Build Turing Machines | |
| Home | Alan TURING | History | Turing machine | The actual experimental prototype | Some diagrams of Turing machines for this prototype | Presentations | Presse | Simulator | A new machine |
|||||||||
| Machines | Ideas | Description | How the machine operates | Technologies | First Turing machine | Easy | Calculations | Sequences | Interesting | Colleges | University | Talks | Videos | Contact | ||||
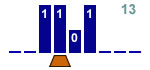
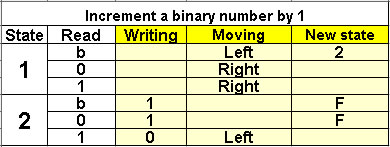
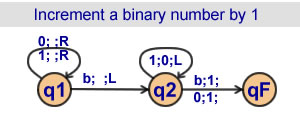
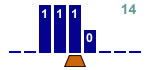
| Increment a binary number by 1 2 states |
 |
 |
 |
 |
|
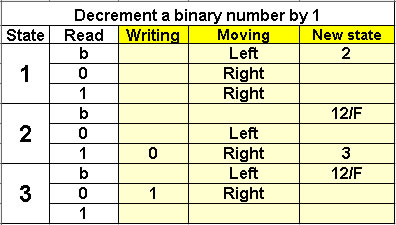
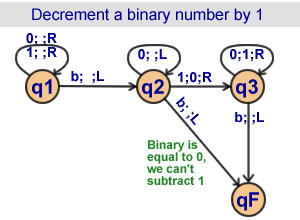
| Decrement a binary number by 1 3 states |
 |
 |
 |
 |
|
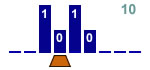
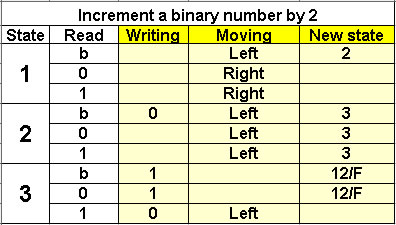
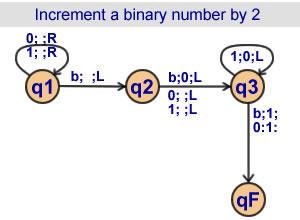
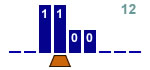
| Increment a binary number by 2 3 states |  |
 |
 |
 |
|
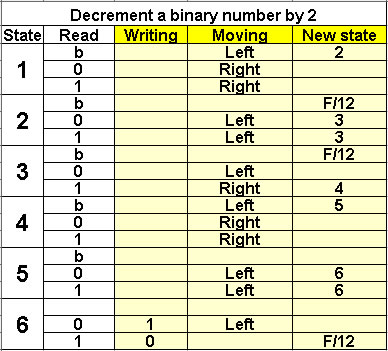
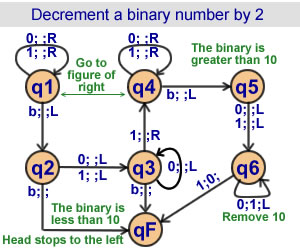
| Decrement a binary number by 2 6 states |
|
 |
 |
|
|
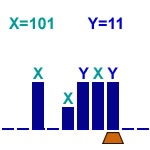
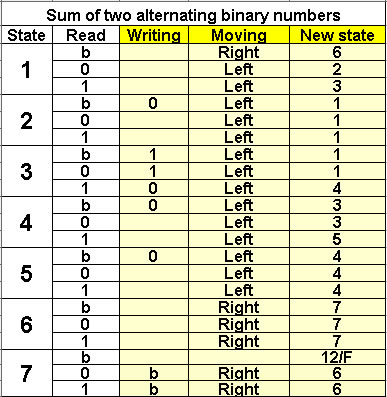
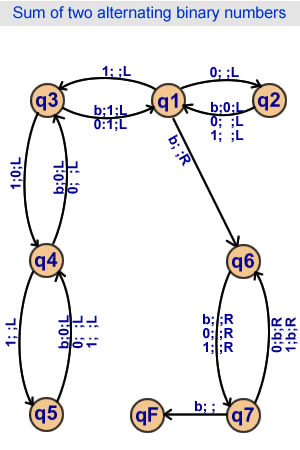
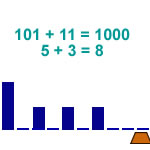
| Sum of two alternating binary numbers 7 states |
 |
 |
 |
 |
|
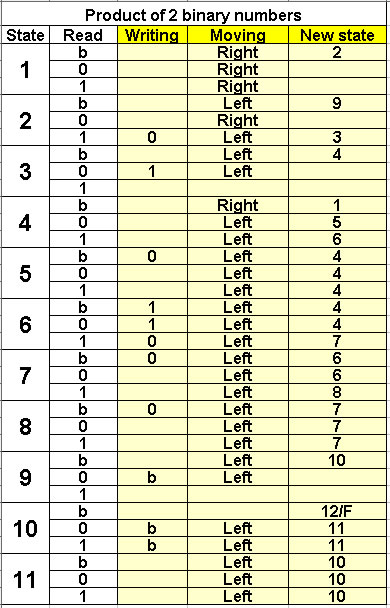
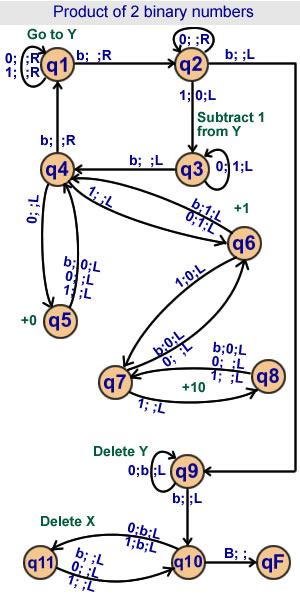
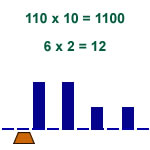
| Product of 2 binary numbers X and Y X is written every other box least significant bit on the right Y : least significant bit on the left 11 states |
 |
 |
 |
 |
|
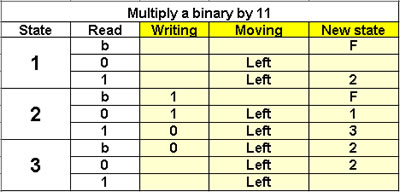
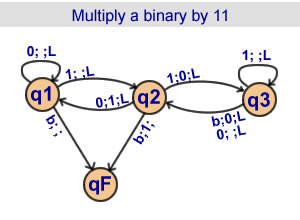
| Calculation of 3n in binary Multiply a binary by 11 3 States |
|
 |
 |
 |
 |
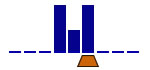
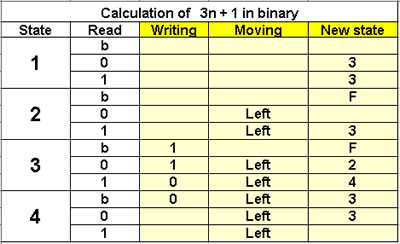
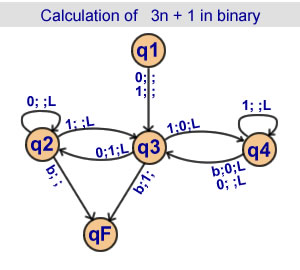
| Calculation of 3n + 1 in binary 4 states |
 |
 |
 |
 |
 |
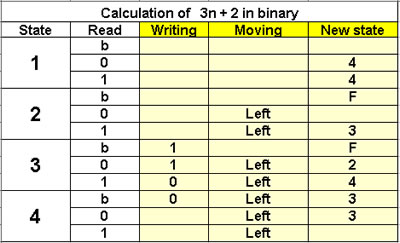
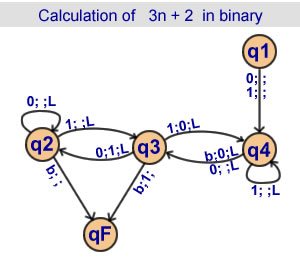
| Calculation of 3n + 2 in binary 4 states |
|
 |
 |
 |
 |
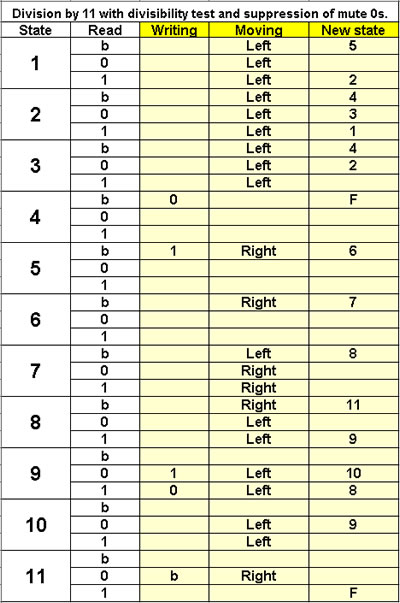
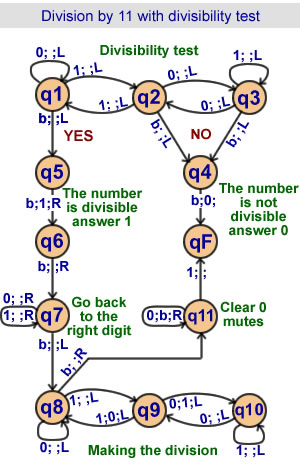
| Division by 11 with divisibility test and suppression of mute 0s. 11 states |
|
|
 |
 |
|
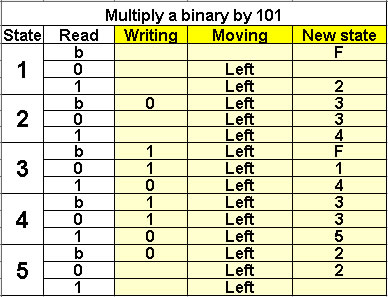
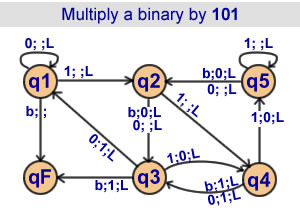
| Calculation of 5n in binary Multiply a binary by 101 5 States |
|
 |
 |
 |
 |
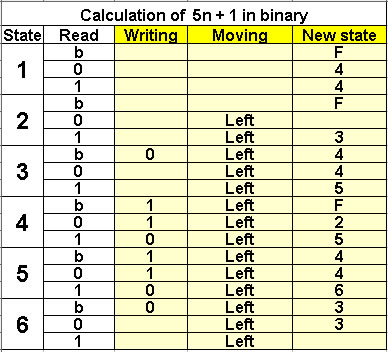
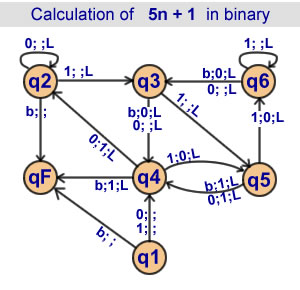
| Calculation of 5n + 1 in binary 6 states |
|
 |
 |
 |
 |
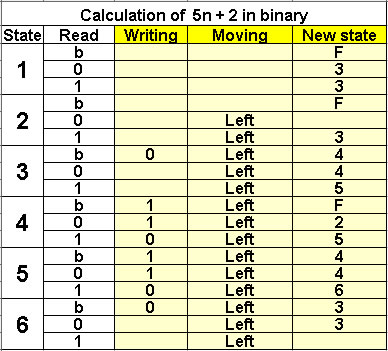
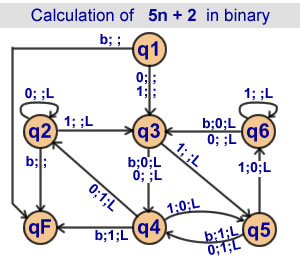
| Calculation of 5n + 2 in binary 6 states |
 |
 |
 |
 |
|
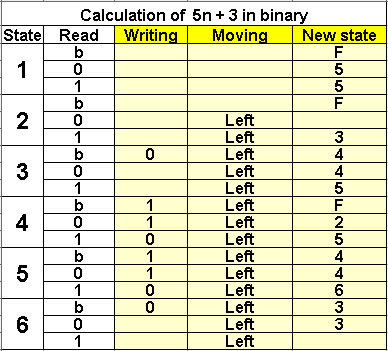
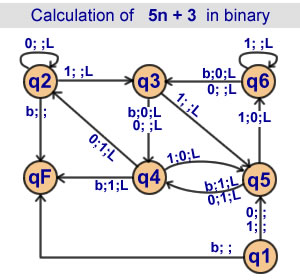
| Calculation of 5n + 3 in binary 6 states |
 |
 |
 |
 |
|
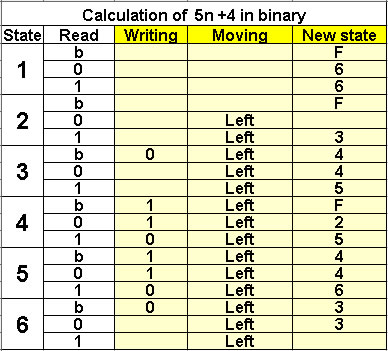
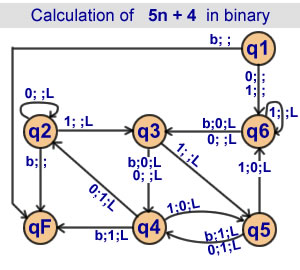
| Calculation of 5n + 4 in binary 6 states |
 |
 |
 |
 |
|
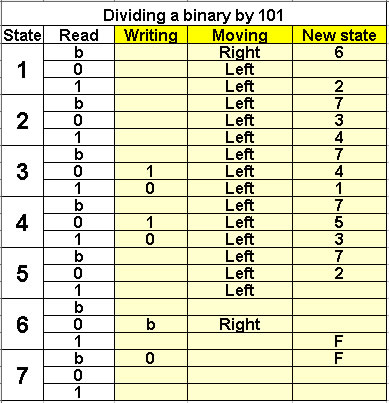
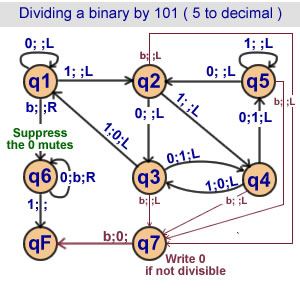
| Dividing a binary by 101 10 states |
|
|
 |
 |
|