|
Un prototype programmable pour concrétiser la machine de Turing | |
| Accueil | Alan TURING | Histoire | Machine de Turing | Le prototype expérimental réalisé | Quelques diagrammes de machines de Turing pour ce prototype | Interventions | Presse | Contact | Nouvelle machine |
|||||||||
| Machines | Idées | Descriptif | Fonctionnement | Technologie | 1ère machine de Turing | Facile | Calculateurs | Suites | Intéressant | Lycées | Universités | Conférences | Vidéos | |||||
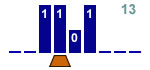
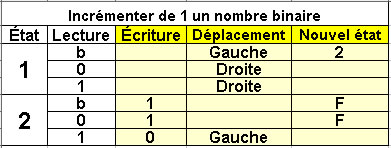
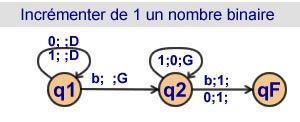
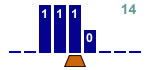
| Incrementer de 1 un nombre binaire 2 états |
 |
 |
 |
 |
|
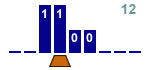
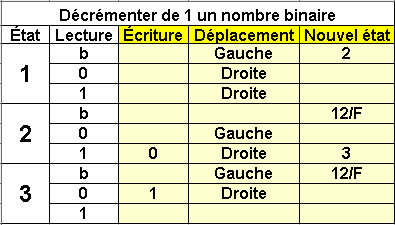
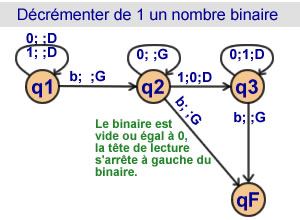
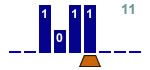
| Décrementer de 1 un nombre binaire 3 états |
 |
 |
 |
 |
|
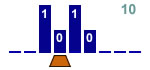
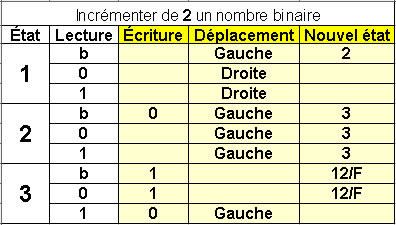
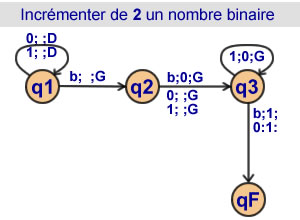
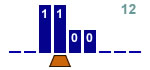
| Incrementer de 2 un nombre binaire 3 états |
 |
 |
 |
 |
|
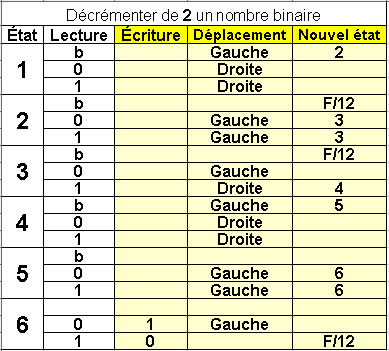
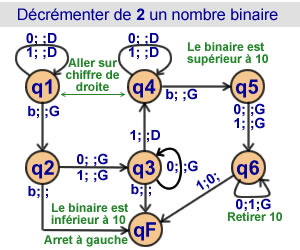
| Decrementer de 2 un nombre binaire 6 états |
|
 |
 |
|
|
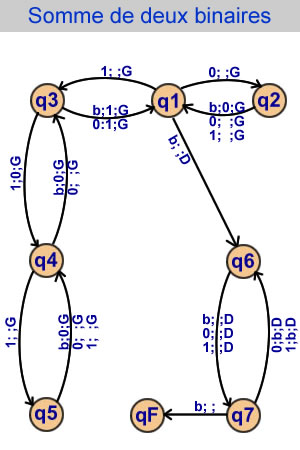
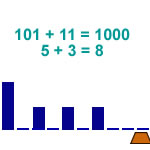
| Somme de deux binaires entremêlés 7 états |
 |
 |
 |
 |
|
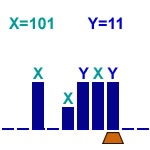
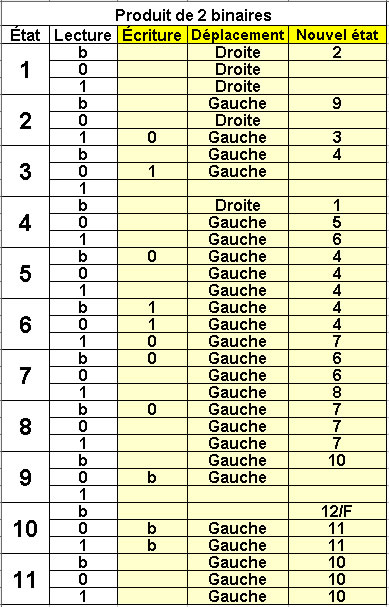
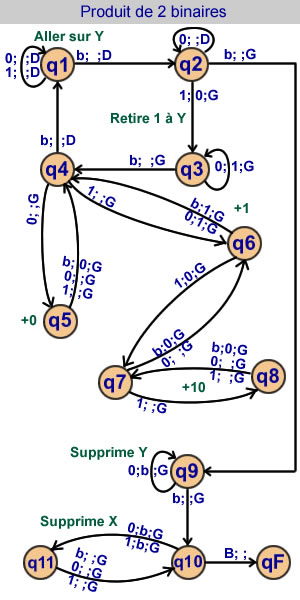
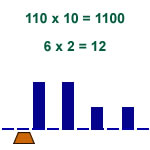
| Produit de 2 nombres binaires X et Y X est écrit une case sur deux bit de poids faible à droite Y : bit de poids faible à gauche 11 états |
 |
 |
 |
 |
|
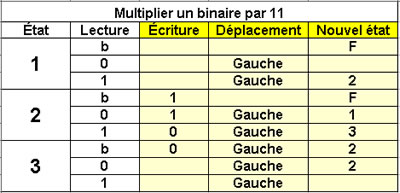
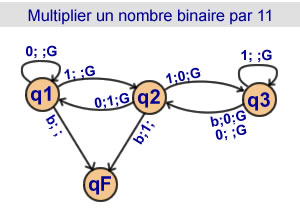
| Calcul de 3n en binaire Multiplier par 11 3 états |
|
 |
 |
 |
 |
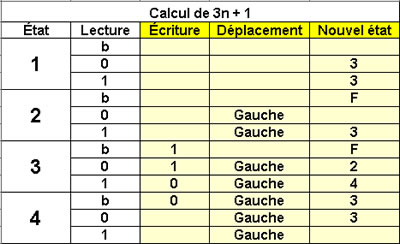
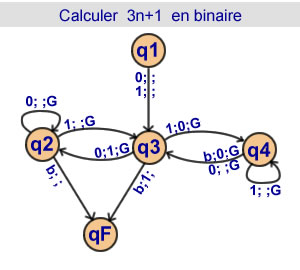
| Calcul de 3n + 1 en binaire
4 états |
 |
 |
 |
 |
 |
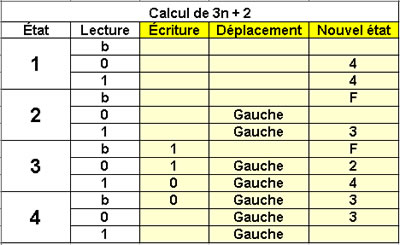
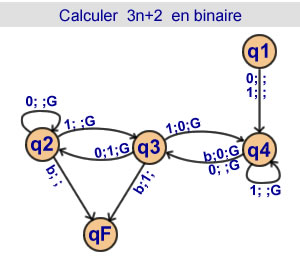
| Calcul de 3n + 2 en binaire
4 états |
|
 |
 |
 |
 |
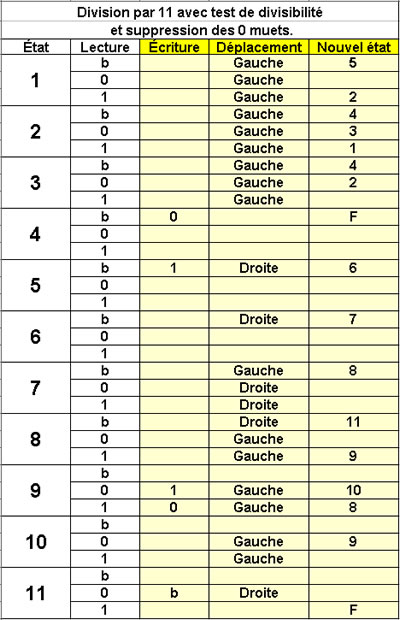
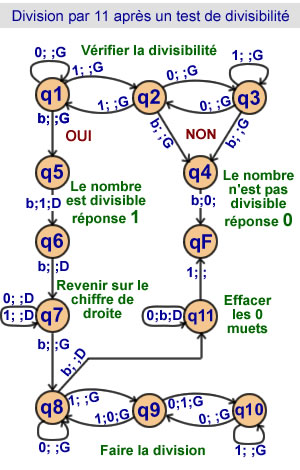
| Division par 11 avec test de divisibilité et suppression des 0 muets. 11 états |
|
|
 |
 |
|
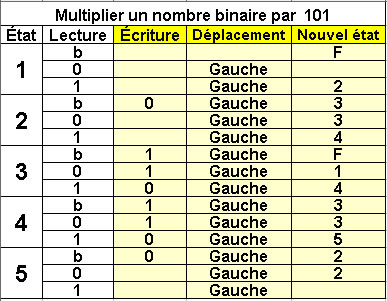
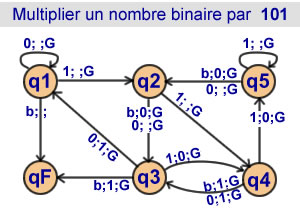
| Calcul de 5n en binaire Multiplier par 101 5 états |
|
 |
 |
 |
 |
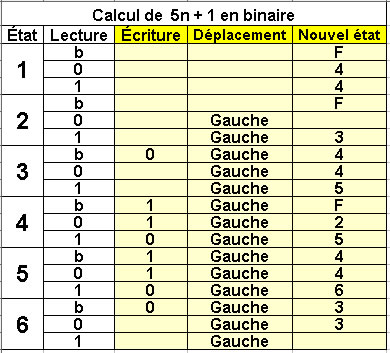
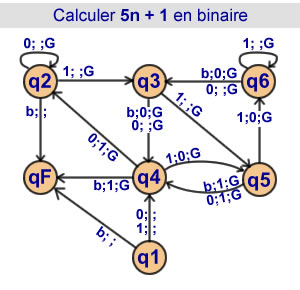
| Calcul de 5n + 1 en binaire 6 états |
|
 |
 |
 |
 |
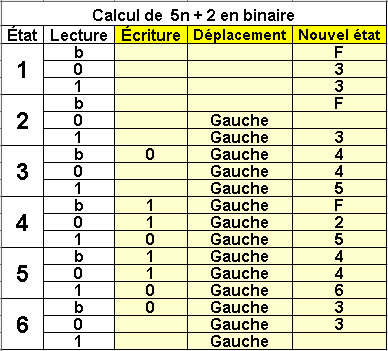
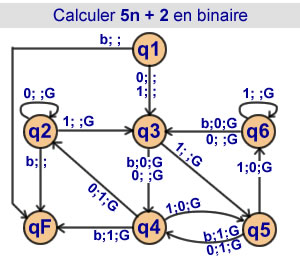
| Calcul de 5n + 2 en binaire 6 états |
 |
 |
 |
 |
|
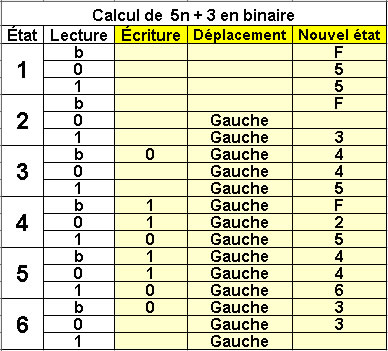
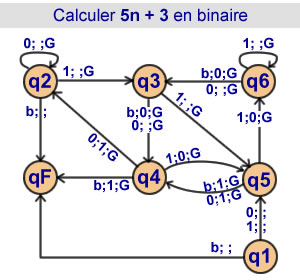
| Calcul de 5n + 3 en binaire 6 états |
 |
 |
 |
 |
|
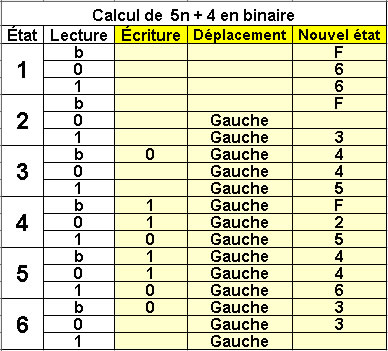
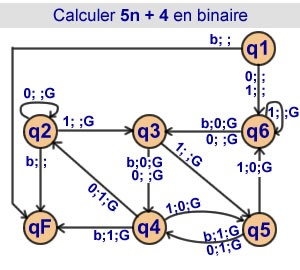
| Calcul de 5n + 4 en binaire 6 états |
 |
 |
 |
 |
|
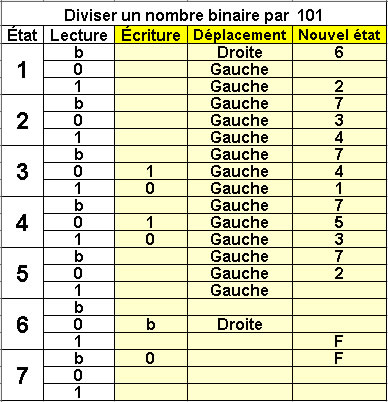
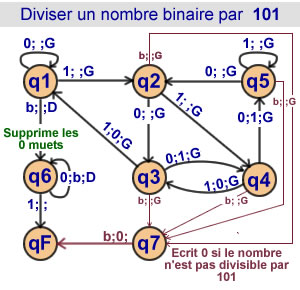
| Division d'un binaire par 101 10 états |
|
|
 |
 |
|